Creazione di istogrammi di distribuzione
Gli istogrammi di distribuzione vengono utilizzati per appurare la variazione mediante la visualizzazione di una curva di distribuzione standard dei valori misurati per un articolo.
Per tracciare questo diagramma, è necessario selezionare una combinazione comprendente articolo o articolo/fornitore, origine dell'ordine di ispezione, elemento caratteristico/caratteristica e il periodo di tempo pertinente. Questo diagramma si basa esclusivamente sui risultati effettivi dell'ispezione.
La linea centrale della curva di distribuzione corrisponde alla media calcolata da LN (µ). I limiti di tolleranza superiore e inferiore del processo sono i limiti entro cui il processo è in grado di produrre componenti di qualità accettabile. Tali limiti di tolleranza sono in genere espressi come media del processo più o meno 3 scostamenti standard (σ) in grado di acquisire il 95% della varianza normale.
Per tracciare questo tipo di diagramma, effettuare le seguenti operazioni:
- Calcolare i valori misurati per un intervallo di periodi.
- Determinare l'escursione R dei valori misurati: R = Xmax – Xmin
- Determinare l'ampiezza di variazione della classe: W = R / SQRT (numero di misure)
- Comporre le classi: Classe 1 Tolleranza inferiore (o Xmin se Xmin < Tolleranza inferiore) quindi Classe 2 = Classe 1 + W e così via
- Popolare le classi in base ai valori misurati. Determinare la frequenza all'interno di ogni classe.
- Calcolare le medie aritmetiche dei valori misurati.
- Calcolare lo scostamento standard.
- Tracciare l'istogramma in base alle classi calcolate.
Esempio
Si supponga che vengano elaborati 5 ordini di ispezione, ognuno con 1 campione, risultanti in un gruppo campione per ogni ordine. Per tutti i 5 ordini di ispezione, la dimensione del campione è di 10 pezzi e la quantità da sottoporre al test è di 1 pezzo. Nella tabella contenente i dati di test vengono visualizzati i risultati riportati di seguito:
| Gruppo campione | Numero di campione | Valore misurato |
| 1 | 1 | 1 |
| 1 | 2 | 1 |
| 1 | 3 | 1,002 |
| 1 | 4 | 0,997 |
| 1 | 5 | 1 |
| 1 | 6 | 1,001 |
| 1 | 7 | 1 |
| 1 | 8 | 1 |
| 1 | 9 | 1 |
| 1 | 10 | 0,999 |
| 2 | 1 | 1 |
| 2 | 2 | 0 |
| 2 | 3 | 0 |
| 2 | 4 | 0 |
| 2 | 5 | 0 |
| 2 | 6 | 0 |
| 2 | 7 | 0 |
| 2 | 8 | 0 |
| 2 | 9 | 0 |
| 2 | 10 | 0 |
| 3 | 1 | 1,001 |
| 3 | 2 | 1 |
| 3 | 3 | 0,9 |
| 3 | 4 | 0,988 |
| 3 | 5 | 1,001 |
| 3 | 6 | 1,004 |
| 3 | 7 | 0,999 |
| 3 | 8 | 0,989 |
| 3 | 9 | 1,012 |
| 3 | 10 | 1,03 |
| 4 | 1 | 1,001 |
| 4 | 2 | 1 |
| 4 | 3 | 0,9 |
| 4 | 4 | 0,988 |
| 4 | 5 | 1,001 |
| 4 | 6 | 1,004 |
| 4 | 7 | 0,999 |
| 4 | 8 | 0,989 |
| 4 | 9 | 1,012 |
| 4 | 10 | 1,03 |
| 5 | 1 | 1,001 |
| 5 | 2 | 1 |
| 5 | 3 | 0,9 |
| 5 | 4 | 0,988 |
| 5 | 5 | 1,001 |
| 5 | 6 | 1,004 |
| 5 | 7 | 0,999 |
| 5 | 8 | 0,989 |
| 5 | 9 | 1,012 |
| 5 | 10 | 1,03 |
Calcolo dell'escursione
Determinare l'escursione dei valori misurati. Il valore massimo misurato è 1,03 (Gruppo campione 1, Numero di campione 10). Il valore minimo misurato è 0,9 (Gruppo campione 1, Numero di campione 3).
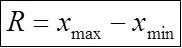
Escursione = 1,03 - 0,9 = 0,13Calcolo dell'ampiezza di variazione della classe
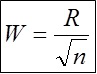
L'ampiezza di variazione della classe è pari a 0,13 / √50 = 0,02055480479109446565799280803881. Questo valore viene arrotondato a 0,02.
Composizione delle classi
Le classi vengono composte come segue: Classe 1 Tolleranza inferiore (o Xmin se Xmin < Tolleranza inferiore) quindi Classe 2 = Classe 1 + W e così via. Vengono generate le classi riportate di seguito:
| Classe 1 | 0,900000 |
| Classe 2 | 0,920000 |
| Classe 3 | 0,940000 |
| Classe 4 | 0,960000 |
| Classe 5 | 0,980000 |
| Classe 6 | 1,000000 |
| Classe 7 | 1,020000 |
Popolamento delle classi
I valori delle diverse misure possono essere raggruppati in una classe, se il valore è pari o superiore al valore della classe e inferiore al valore della classe più l'ampiezza di variazione della classe. Il risultato è il seguente:
| Classe | Numero di misure |
| 1 | 1 |
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 12 |
| 6 | 36 |
| 7 | 1 |
Calcolo della media
Per ogni misura, viene calcolata la differenza rispetto alla media e vengono sommati tra loro i quadrati delle differenze. Se il valore della misura del primo numero di campione è 1:
(1 - 0,995850)² = (0,00415)² = 0,0000172225Le differenze al quadrato vengono calcolate e sommate tra loro per determinare una differenza al quadrato totale. Nel caso dell'esempio sopra riportato il totale è 1,311734.
Media = Scostamento standard - √ 1,311734 /
50 = 0,160000Tracciatura del diagramma
Nella figura riportata di seguito è illustrato il diagramma tracciato con i dati sopra riportati:
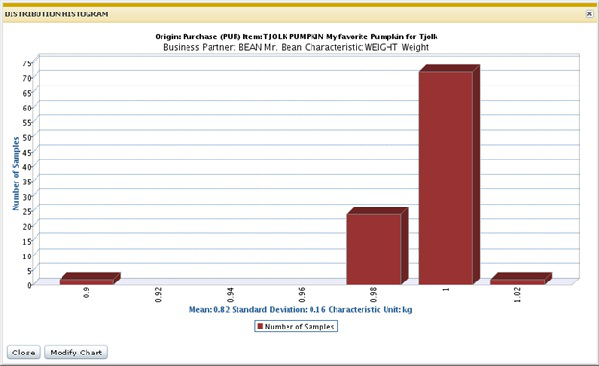
Sull'asse X è visualizzata l'unità di misura della caratteristica. È tuttavia possibile che per una procedura di test standard specifica o per una riga di un ordine di ispezione il valore della misura venga espresso in un'unità diversa e successivamente convertito nell'unità di misura della caratteristica.