Crear histogramas de distribución
Los histogramas de distribución se utilizan para verificar la variación mostrando una curva de distribución estándar de valores medidos para un artículo.
Para trazar este gráfico debe seleccionar la combinación de artículo o artículo/proveedor, el origen de orden de inspección y el aspecto/la característica, así como el período de tiempo correspondiente. Este gráfico se basa únicamente en resultados de inspección reales.
La línea central de la curva de distribución es la media calculada (µ) de LN. Los límites de tolerancia por encima o por debajo del proceso son los límites dentro de los cuales el proceso es capaz de producir piezas de una calidad aceptable. Estos límites de tolerancia se suelen expresar como la media del proceso más o menos 3 desviaciones estándar (σ) que pueden capturar el 95% de la distribución de variación normal.
Para trazar este tipo de gráfico, realice los pasos siguientes:
- Calcular los valores medidos para un rango de períodos
- Determinar la distribución R de los valores medidos: R = Xmax – Xmin
- Determinar la anchura de clase: W = R / SQRT (número de medidas)
- Componer las clases: Si Tolerancia inferior de clase 1 (o Xmin en caso de que Xmin < Tolerancia inferior), entonces Clase2 = Clase1 + W y así sucesivamente
- Rellenar las clases basándose en los valores medidos. Determinar la frecuencia dentro de cada clase
- Calcular la media aritmética de los valores medidos
- Calcular la desviación estándar
- Trazar el histograma basado en las clases calculadas
Ejemplo
Suponga que se procesan 5 órdenes de inspección, cada una con 1 muestra, lo que produce un grupo de muestras para cada orden. Las 5 órdenes de inspección tienen un tamaño de muestra de 10 piezas y una cantidad de prueba de 1 pieza. Se muestran los siguientes resultados en la tabla de datos de prueba:
| Grupo de muestras | Número de muestra | Valor medido |
| 1 | 1 | 1 |
| 1 | 2 | 1 |
| 1 | 3 | 1,002 |
| 1 | 4 | 0,997 |
| 1 | 5 | 1 |
| 1 | 6 | 1,001 |
| 1 | 7 | 1 |
| 1 | 8 | 1 |
| 1 | 9 | 1 |
| 1 | 10 | 0,999 |
| 2 | 1 | 1 |
| 2 | 2 | 0 |
| 2 | 3 | 0 |
| 2 | 4 | 0 |
| 2 | 5 | 0 |
| 2 | 6 | 0 |
| 2 | 7 | 0 |
| 2 | 8 | 0 |
| 2 | 9 | 0 |
| 2 | 10 | 0 |
| 3 | 1 | 1,001 |
| 3 | 2 | 1 |
| 3 | 3 | 0,9 |
| 3 | 4 | 0,988 |
| 3 | 5 | 1,001 |
| 3 | 6 | 1,004 |
| 3 | 7 | 0,999 |
| 3 | 8 | 0,989 |
| 3 | 9 | 1,012 |
| 3 | 10 | 1,03 |
| 4 | 1 | 1,001 |
| 4 | 2 | 1 |
| 4 | 3 | 0,9 |
| 4 | 4 | 0,988 |
| 4 | 5 | 1,001 |
| 4 | 6 | 1,004 |
| 4 | 7 | 0,999 |
| 4 | 8 | 0,989 |
| 4 | 9 | 1,012 |
| 4 | 10 | 1,03 |
| 5 | 1 | 1,001 |
| 5 | 2 | 1 |
| 5 | 3 | 0,9 |
| 5 | 4 | 0,988 |
| 5 | 5 | 1,001 |
| 5 | 6 | 1,004 |
| 5 | 7 | 0,999 |
| 5 | 8 | 0,989 |
| 5 | 9 | 1,012 |
| 5 | 10 | 1,03 |
Calcular la distribución
Determine la distribución de los valores medidos. El mayor valor medido es de 1,03 (Grupo de muestras 1, Número de muestra 10). El menor valor medido es de 0,9 (Grupo de muestras 1, Número de muestra 3).
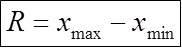
Distribución = 1,03 – 0,9 = 0,13Calcular la anchura de clase:
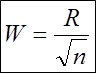
La anchura de clase es 0,13 / √50 = 0,02055480479109446565799280803881. Este valor se redondea a 0,02.
Componer las clases
Las clases se componen de la siguiente manera: Si Tolerancia inferior de clase 1 (o Xmin en caso de que Xmin < Tolerancia inferior), entonces Clase2 = Clase1 + W y así sucesivamente. Se generan las clases siguientes:
| Clase 1 | 0,900000 |
| Clase 2 | 0,920000 |
| Clase 3 | 0,940000 |
| Clase 4 | 0,960000 |
| Clase 5 | 0,980000 |
| Clase 6 | 1,000000 |
| Clase 7 | 1,020000 |
Cumplimentar las clases
Los valores de las distintas medidas se pueden agrupar en una clase, si el valor es mayor o igual que el valor de la clase, y menor que el valor de la clase + la anchura de la clase. El resultado es:
| Clase | Número de medidas |
| 1 | 1 |
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 12 |
| 6 | 36 |
| 7 | 1 |
Calcular la media
Para cada medida, se calcula la diferencia en la media y se suman los cuadrados de las diferencias. Si el primer número de muestra tiene un valor de medida de 1:
(1 - 0,995850)² = (0,00415)² = 0,0000172225Se calculan las diferencias de los cuadrados y se suman para formar la diferencia de cuadrados total. Para el ejemplo anterior el total es 1,311734.
Media = Desviación estándar - √ 1,311734 /
50 = 0,160000Trazar el gráfico
La figura siguiente muestra el gráfico trazado con los datos anteriores:
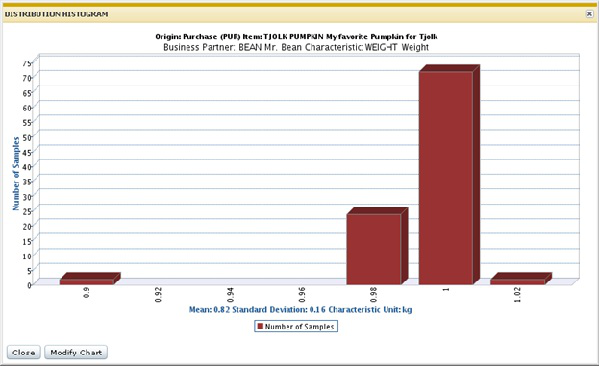
En el eje X se muestra la unidad de características. Sin embargo, puede que para un procedimiento de prueba estándar específico o para una línea de orden de inspección, el valor de la medida se exprese en una unidad diferente que se convierte más adelante a la unidad de característica.