Método de previsión: regresión polinómica
Los parámetros relevantes para este método de previsión son:
- Grado de regresión polinómica
- Tipo de influencia estacional
- Tiempo de ciclo estacional
- Actualización automática de parámetros de previsión
Puede mantener estos parámetros en la sesión Artículos de planificación - Configuración de previsión (cpdsp1110m000).
El grado del polinomio viene indicado por el campo Grado de regresión polinómica. Si la casilla de verificación Actualización automática de parámetros de previsión está seleccionada, LN determina el grado óptimo del polinomio.
Demanda media con tendencia corregida
En primer lugar, las cifras históricas de demanda se corrigen con la demanda media con tendencia corregida para el período pertinente.
Sin influencia estacional:
TD(t) = AVCon una influencia de tendencia lineal:
TD(t) = CS + TF * tCon una influencia de tendencia progresiva:
TD(t) = BS * TF ^ (t-1)DM(t) = AD(t) - TD(t)Donde:
| DM(t) | demanda media con tendencia corregida para el período t |
| TD(t) | demanda basada en tendencia para el período t |
| AD(t) | demanda real para el período t |
| AV | demanda media (*) |
| CS | demanda constante |
| BS | demanda estimada para el período 1 |
| TF | factor de tendencia |
(*) La demanda media es la suma de las cifras de demanda históricas por período, dividida por el número de períodos con historia de demanda.
Coeficientes del polinomio
LN calcula los coeficientes del polinomio con el método de regresión polinómica. Consulte los temas relacionados para obtener más información sobre regresión polinómica.
Previsión de demanda
LN calcula la demanda de cada período de previsión según la demanda media con tendencia corregida para el período en cuestión, incrementada con el ruido medio en el pasado.
Ruido
El ruido es la fluctuación de los datos de demanda comparados con la tendencia que se ha determinado. El ruido medio se determina para cada período de previsión según los períodos históricos, que son un número completo de ciclos estacionales.
Si el campo Tipo de influencia estacional es No aplicable, LN supone un ciclo estacional ficticio con una longitud de estación de hasta una cuarta parte del número de períodos con demanda histórica.
Ejemplo
En este diagrama se muestran los datos históricos de demanda de dos ciclos estacionales, que constan de 8 períodos de previsión. El período 9 es el período actual.
SCT = tiempo de ciclo estacional
En este diagrama se muestra el polinomio determinado mediante regresión polinómica.
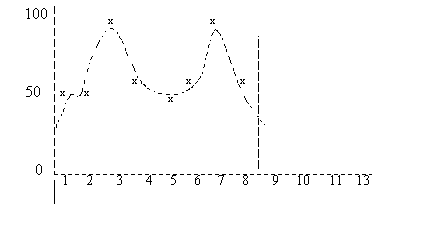
Para cada período histórico, la demanda basada en el polinomio se compara con la tendencia de la demanda. Se supone que hay una tendencia lineal, caracterizada por la fórmula siguiente:
TD(t) = CS + TF * t| TD (t) | demanda basada en tendencia para el período t |
| CS | demanda constante (= 54) |
| TF | factor de tendencia (= 2) |
| Período | Polinomio | Tendencia | Ruido |
|---|---|---|---|
| 1 | 45 | 56 | -11 |
| 2 | 53 | 58 | -5 |
| 3 | 76 | 60 | +16 |
| 4 | 70 | 62 | +8 |
| 5 | 49 | 64 | -15 |
| 6 | 55 | 66 | -11 |
| 7 | 78 | 68 | +10 |
| 8 | 70 | 70 | +0 |
El ruido medio basado en esas diferencias se añade a la demanda con tendencia corregida. Por ejemplo, el ruido medio para el período de previsión 9 es el promedio del ruido de los períodos 1 y 5.
| Período de previsión | Tendencia | Ruido medio | Basado en períodos | Demanda de previsión |
|---|---|---|---|---|
| 9 | 72 | -13 | 1,5 | 59 |
| 10 | 74 | -8 | 2,6 | 66 |
| 11 | 76 | +13 | 3,7 | 89 |
| 12 | 78 | +4 | 4,8 | 82 |
| 13 | 80 | -13 | 1,4 | 67 |
| 14 | 82 | -7 | 2,6 | 75 |
En este diagrama se muestra el resultado: