Erstellen von Verteilungshistogrammen
Verteilungshistogramme dienen der Bestimmung von Abweichungen. Dazu wird eine voreingestellte Verteilungskurve der gemessenen Werte für einen Artikel angezeigt.
Zum Plotten des Diagramms müssen Sie die Kombination aus Artikel oder Artikel/Lieferant, Prüfauftragsursprung, Aspekt/Merkmal und den relevanten Zeitraum auswählen. Das Diagramm basiert ausschließlich auf tatsächlichen Prüfergebnissen.
Der zentrale Wert der Verteilungskurve ist der berechnete LN Durchschnitt (µ). Die oberen/unteren Toleranzgrenzen des Prozesses sind die Grenzwerte, innerhalb der der Prozess fähig ist, Teile mit einer akzeptablen Qualität zu produzieren. Diese Toleranzgrenzen werden im Allgemeinen als Prozessdurchschnitt plus/minus 3 Standardabweichungen (σ) angegeben, die 95% der normalen Abweichungsverteilung erfassen.
Gehen Sie folgendermaßen vor, um diese Diagrammart zu plotten:
- Berechnen Sie gemessene Werte für einen Bereich von Perioden.
- Bestimmen Sie die Verteilung R der gemessenen Werte: R = Xmax – Xmin
- Bestimmen Sie die Klassenbreite: W = R / SQRT (Anzahl der Messungen)
- Stellen Sie die Klassen zusammen: Klasse1 untere Toleranz (oder Xmin falls Xmin < untere Toleranz), dann Klasse2 = Klasse1 + W usw.
- Befüllen Sie die Klassen basierend auf den gemessenen Werten. Bestimmen Sie die Häufigkeit innerhalb der einzelnen Klassen.
- Berechnen Sie den arithmetischen Durchschnitt der gemessenen Werte.
- Berechnen Sie die Standardabweichung.
- Plotten Sie das Histogramm basierend auf den berechneten Klassen.
Beispiel
Angenommen, es wurden 5 Prüfaufträge mit jeweils 1 Stichprobe verarbeitet, sodass eine Stichprobengruppe für jeden Auftrag vorhanden ist. Alle 5 Prüfaufträge haben einen Stichprobenumfang von 10 Stück und eine Prüfmenge von 1 Stück. In der Prüfdatentabelle werden folgende Ergebnisse angezeigt:
| Stichprobengruppe | Stichprobennummer | Gemessener Wert |
| 1 | 1 | 1 |
| 1 | 2 | 1 |
| 1 | 3 | 1,002 |
| 1 | 4 | 0,997 |
| 1 | 5 | 1 |
| 1 | 6 | 1,001 |
| 1 | 7 | 1 |
| 1 | 8 | 1 |
| 1 | 9 | 1 |
| 1 | 10 | 0,999 |
| 2 | 1 | 1 |
| 2 | 2 | 0 |
| 2 | 3 | 0 |
| 2 | 4 | 0 |
| 2 | 5 | 0 |
| 2 | 6 | 0 |
| 2 | 7 | 0 |
| 2 | 8 | 0 |
| 2 | 9 | 0 |
| 2 | 10 | 0 |
| 3 | 1 | 1,001 |
| 3 | 2 | 1 |
| 3 | 3 | 0,9 |
| 3 | 4 | 0,988 |
| 3 | 5 | 1,001 |
| 3 | 6 | 1,004 |
| 3 | 7 | 0,999 |
| 3 | 8 | 0,989 |
| 3 | 9 | 1,012 |
| 3 | 10 | 1,03 |
| 4 | 1 | 1,001 |
| 4 | 2 | 1 |
| 4 | 3 | 0,9 |
| 4 | 4 | 0,988 |
| 4 | 5 | 1,001 |
| 4 | 6 | 1,004 |
| 4 | 7 | 0,999 |
| 4 | 8 | 0,989 |
| 4 | 9 | 1,012 |
| 4 | 10 | 1,03 |
| 5 | 1 | 1,001 |
| 5 | 2 | 1 |
| 5 | 3 | 0,9 |
| 5 | 4 | 0,988 |
| 5 | 5 | 1,001 |
| 5 | 6 | 1,004 |
| 5 | 7 | 0,999 |
| 5 | 8 | 0,989 |
| 5 | 9 | 1,012 |
| 5 | 10 | 1,03 |
Verteilung berechnen
Bestimmen Sie die Verteilung der gemessenen Werte. Der höchste gemessene Wert ist 1,03 (Stichprobengruppe 1, Stichprobennummer 10). Der niedrigste gemessene Wert ist 0,9 (Stichprobengruppe 1, Stichprobennummer 3).
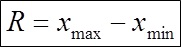
Verteilung = 1,03 - 0,9 = 0,13Klassenbreite berechnen:
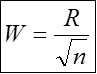
Die Klassenbreite ist 0,13 / √50 = 0,02055480479109446565799280803881. Dieser Wert wird auf 0,02 gerundet.
Klassen zusammenstellen
Die Klassen werden wie folgt zusammengestellt: Klasse1 untere Toleranz (oder Xmin falls Xmin < untere Toleranz), dann Klasse2 = Klasse1 + W usw. Folgende Klassen werden generiert:
| Klasse 1 | 0,900000 |
| Klasse 2 | 0,920000 |
| Klasse 3 | 0,940000 |
| Klasse 4 | 0,960000 |
| Klasse 5 | 0,980000 |
| Klasse 6 | 1,000000 |
| Klasse 7 | 1,020000 |
Klassen befüllen
Die Werte der unterschiedlichen Messungen können in einer Klasse zusammengefasst werden, falls der Wert größer oder gleich dem Klassenwert und weniger als der Klassenwert + Klassenbreite ist. Das Ergebnis lautet wie folgt:
| Klasse | Anzahl der Messungen |
| 1 | 1 |
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 12 |
| 6 | 36 |
| 7 | 1 |
Durchschnitt berechnen
Für jede Messung wird die Differenz zum Durchschnitt berechnet und der Quadratwert der Differenzen addiert. Angenommen, die erste Stichprobennummer hat einen Messwert von 1:
(1 - 0,995850)² = (0,00415)² = 0,0000172225Die Quadrate der Differenzen werden berechnet und addiert und bilden die Summe der Quadratdifferenzen. Im obigen Beispiel ist die Summe 1,311734.
Durchschnitt = Standardabweichung - √ 1,311734 /
50 = 0,160000Diagramm plotten
Die nachfolgende Abbildung zeigt das geplottete Diagramm mit den obigen Daten:
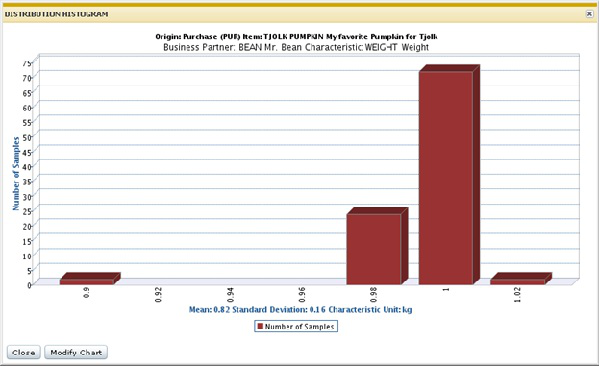
Auf der X-Achse wird die Merkmalseinheit angezeigt. Es ist jedoch möglich, den Messwert für ein bestimmtes Standardprüfverfahren oder für eine Prüfauftragsposition in einer anderen Einheit anzugeben und diese später in die Einheit des Merkmals umzurechnen.