Prognoseverfahren: Polynomische Regression
Folgende Parameter werden bei diesem Prognoseverfahren zugrunde gelegt:
- Grad Polynomen-Regression
- Art des Saisoneinflusses
- Saisonzyklus in Perioden
- Prognoseparameter automatisch aktualisieren
Diese Parameter können Sie im Programm Planartikel - Prognoseeinstellungen (cpdsp1110m000) verwalten.
Der Grad des Polynoms wird im Feld Grad Polynomen-Regression angegeben. Wenn das Kontrollkästchen Prognoseparameter automatisch aktualisieren markiert ist, bestimmt LN den optimalen Grad des Polynoms.
Trendangepasster durchschnittlicher Bedarf
Zunächst werden die historischen Bedarfsdaten anhand des trendangepassten durchschnittlichen Bedarfs für die relevante Periode angepasst.
Ohne saisonale Schwankungen:
TB(t) = DBMit linearem Trendeinfluss:
TB(t) = KB + TF * tMit progressivem Trendeinfluss:
TB(t) = BB * TF ^ (t-1); TdB(t) = TaB(t) - TB(t)Erläuterung
| TdB(t) | trend-angepasster durchschnittlicher Bedarf für Periode t |
| TB(t) | trendbasierter Bedarf für Periode t |
| TaB(t) | tatsächlicher Bedarf für Periode t |
| DB | durchschnittlicher Bedarf (*) |
| KB | konstanter Bedarf |
| BB | vorkalkulierter Bedarf für Periode 1 |
| TF | Trendfaktor |
(*) Der durchschnittliche Bedarf wird als die Summe der historischen Bedarfsdaten pro Periode geteilt durch die Anzahl der Perioden mit Bedarfshistorie ermittelt.
Polynomkoeffizienten
LN ermittelt die Koeffizienten des Polynoms anhand des Verfahrens der polynomischen Regression. Weitere Informationen zur polynomischen Regression finden Sie in den entsprechenden Themen.
Bedarfsprognose
LN berechnet den Bedarf für jede Prognoseperiode auf der Grundlage des trendangepassten durchschnittlichen Bedarfs für die betreffende Periode zuzüglich des durchschnittlichen Störfaktors der Vergangenheit.
Störfaktor
Der Störfaktor ist die Fluktuation der Bedarfsdaten im Vergleich zum ermittelten Trend. Der durchschnittliche Störfaktor wird für jede Prognoseperiode auf der Grundlage der Historieperioden ermittelt, die eine ganze Zahl von Saisonzyklen zurückliegen.
Wenn das Feld Art des Saisoneinflusses auf --- gesetzt ist, nimmt LN einen fiktiven Saisonzyklus mit einer Länge von bis zu einem Viertel der Perioden an, für die eine Bedarfshistorie vorliegt.
Beispiel
Dieses Diagramm zeigt die historischen Bedarfsdaten zweier Saisonzyklen mit 8 Prognoseperioden. Periode 9 ist die aktuelle Periode.
SZP = Saisonzyklus in Perioden
Das Diagramm zeigt das Polynom, das anhand polynomischer Regression ermittelt wurde.
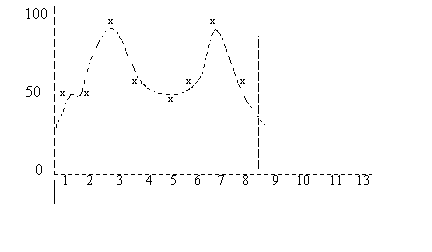
Für jede Periode der Historie wird der auf dem Polynom basierende Bedarf mit dem Bedarfstrend verglichen. Es wird ein linearer Trend vorausgesetzt, der durch die folgende Formel ausgedrückt wird:
TB(t) = KB + TF * t| TB (t) | trendbasierter Bedarf für Periode t |
| KB | konstanter Bedarf (= 54) |
| TF | Trendfaktor (= 2) |
| Periode | Polynom | Trend | Störfaktor |
|---|---|---|---|
| 1 | 45 | 56 | -11 |
| 2 | 53 | 58 | -5 |
| 3 | 76 | 60 | +16 |
| 4 | 70 | 62 | +8 |
| 5 | 49 | 64 | -15 |
| 6 | 55 | 66 | -11 |
| 7 | 78 | 68 | +10 |
| 8 | 70 | 70 | +0 |
Der auf diesen Differenzen basierende durchschnittliche Störfaktor wird zum trendangepassten Bedarf addiert. Beispiel: Der durchschnittliche Störfaktor für die Prognoseperiode 9 entspricht dem Durchschnitt der Störfaktoren der Perioden 1 und 5.
| Prognoseperiode | Trend | Durchschnittlicher Störfaktor | Basierend auf Perioden | Bedarfsprognose |
|---|---|---|---|---|
| 9 | 72 | -13 | 1,5 | 59 |
| 10 | 74 | -8 | 2,6 | 66 |
| 11 | 76 | +13 | 3,7 | 89 |
| 12 | 78 | +4 | 4,8 | 82 |
| 13 | 80 | -13 | 1,4 | 67 |
| 14 | 82 | -7 | 2,6 | 75 |
Im folgenden Diagramm ist das Ergebnis dargestellt: