预测方法:多项式回归
LN 将根据“多项式回归”预测方法,依据与历史需求数据匹配的 n 次回归多项式计算需求预测。
此预测方法的相关参数包括:
- “多项式回归的次数”
- “季节性变化类型 ”
- “季节性周期”
- “自动更新预测参数”
可以在“按计划物料列出的预测设置 (cpdsp1110m000)”进程中维护这些参数。
多项式的次数由“多项式回归的次数”字段指示。如果选中了“自动更新预测参数”复选框,则由 LN 确定多项式的最佳次数。
按趋势进行调整的平均需求
首先,根据按趋势进行调整的相关期段平均需求调整历史需求数据。
没有季节性变化:
TD(t) = AV具有线性趋势变化:
TD(t) = CS + TF * t具有递增趋势变化:
TD(t) = BS * TF ^ (t-1)DM(t) = AD(t) - TD(t)其中,
| DM(t) | 按趋势进行调整的期段 t 的平均需求 |
| TD(t) | 期段 t 的基于趋势的需求 |
| AD(t) | 期段 t 的实际需求 |
| AV | 平均需求 (*) |
| CS | 固定需求 |
| BS | 期段 1 的估计需求 |
| TF | 趋势因子 |
(*) 平均需求是期段的历史需求数字的总和除以具有需求历史记录的期段数。
多项式的系数
LN 将采用多项式回归方法计算多项式的系数。如需有关多项式回归的更多信息,请参阅相关主题。
需求预测
LN 基于按趋势进行调整的当前期段平均需求计算每个预测期段的需求;该平均需求在过去随平均波动而增长。
波动
波动指需求数据相对于已确定趋势的波动幅度。每个预测期段的平均波动都依据整数个季节性周期之前的历史期段数确定。
注意
如果“季节性变化类型 ”字段为“不适用”,LN 将假定一个虚构的季节性周期,其季节长度不超过具有历史需求的期段数的四分之一。
示例
下图显示两个季节性周期的历史需求数据,共由 8 个预测期段组成。期段 9 为当前期段。
SCT = 季节性周期
下图显示通过多项式回归确定的多项式。
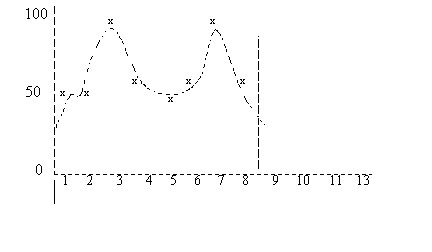
对于每个历史期段,都会对基于多项式的需求与需求的趋势进行比较。假定存在线性趋势,计算公式如下:
TD(t) = CS + TF * t| TD (t) | 期段 t 的基于趋势的需求 |
| CS | 固定需求 (= 54) |
| TF | 趋势因子 (= 2) |
| 期段 | 多项式 | 趋势 | 波动 |
|---|---|---|---|
| 1 | 45 | 56 | -11 |
| 2 | 53 | 58 | -5 |
| 3 | 76 | 60 | +16 |
| 4 | 70 | 62 | +8 |
| 5 | 49 | 64 | -15 |
| 6 | 55 | 66 | -11 |
| 7 | 78 | 68 | +10 |
| 8 | 70 | 70 | +0 |
将基于这些差异的平均波动加到按趋势进行调整的需求中。例如,预测期段 9 的平均波动为期段 1 和 5 的波动平均值。
| 预测期段 | 趋势 | 平均波动 | 基于期段 | 预测需求 |
|---|---|---|---|---|
| 9 | 72 | -13 | 1.5 | 59 |
| 10 | 74 | -8 | 2.6 | 66 |
| 11 | 76 | +13 | 3.7 | 89 |
| 12 | 78 | +4 | 4.8 | 82 |
| 13 | 80 | -13 | 1.4 | 67 |
| 14 | 82 | -7 | 2.6 | 75 |
下图显示结果: