Para criar histogramas de distribuição
Histogramas de distribuição são usados para determinar a variação, exibindo uma curva de distribuição padrão dos valores medidos para um item.
Para plotar esse gráfico, é necessário selecionar a combinação de item ou item/fornecedor, origem da ordem de inspeção, aspecto/característica, bem como o período relevante. Esse gráfico se baseia somente em resultados reais de inspeção.
A linha central da curva de distribuição é a média calculada (µ) do LN. Os limites de tolerância superior/inferior do processo são os limites em que o processo é capaz de produzir peças de qualidade aceitável. Esses limites de tolerância geralmente são expressos como a média do processo mais ou menos três desvios padrão (σ) que pode capturar 95% da distribuição normal de variância.
Para plotar esse tipo de gráfico, execute os seguintes passos:
- Calcule os valores medidos para um intervalo de períodos.
- Determina a distribuição R dos valores medidos: R = Xmax – Xmin
- Determine a largura da classe: W = R / SQRT (nº de medições)
- Componha a classe: Tolerância inferior da classe 1 (ou Xmin em caso de Xmin < tolerância inferior) então Classe2 = Classe1 + W, e assim por diante
- Preencha as classes com base nos valores medidos. Determine a frequência dentro de cada classe.
- Calcule as médias aritméticas dos valores medidos.
- Calcule o desvio padrão.
- Faça a plotagem do histograma com base nas classes calculadas.
Exemplo
Suponha que 5 ordens de inspeção sejam processadas, cada uma com 1 amostra, resultando em um grupo de amostras para cada ordem. Todas as 5 ordens de inspeção têm um tamanho de amostra de 10 peças e uma quantidade de teste de 1 peça. Os seguintes resultados são exibidos na tabela de dados de teste:
| Grupo de amostras | Nº da amostra | Valor medido |
| 1 | 1 | 1 |
| 1 | 2 | 1 |
| 1 | 3 | 1,002 |
| 1 | 4 | 0,997 |
| 1 | 5 | 1 |
| 1 | 6 | 1.001 |
| 1 | 7 | 1 |
| 1 | 8 | 1 |
| 1 | 9 | 1 |
| 1 | 10 | 0.999 |
| 2 | 1 | 1 |
| 2 | 2 | 0 |
| 2 | 3 | 0 |
| 2 | 4 | 0 |
| 2 | 5 | 0 |
| 2 | 6 | 0 |
| 2 | 7 | 0 |
| 2 | 8 | 0 |
| 2 | 9 | 0 |
| 2 | 10 | 0 |
| 3 | 1 | 1.001 |
| 3 | 2 | 1 |
| 3 | 3 | 0.9 |
| 3 | 4 | 0.988 |
| 3 | 5 | 1.001 |
| 3 | 6 | 1.004 |
| 3 | 7 | 0.999 |
| 3 | 8 | 0.989 |
| 3 | 9 | 1.012 |
| 3 | 10 | 1.03 |
| 4 | 1 | 1.001 |
| 4 | 2 | 1 |
| 4 | 3 | 0.9 |
| 4 | 4 | 0.988 |
| 4 | 5 | 1.001 |
| 4 | 6 | 1.004 |
| 4 | 7 | 0.999 |
| 4 | 8 | 0.989 |
| 4 | 9 | 1.012 |
| 4 | 10 | 1.03 |
| 5 | 1 | 1.001 |
| 5 | 2 | 1 |
| 5 | 3 | 0.9 |
| 5 | 4 | 0.988 |
| 5 | 5 | 1.001 |
| 5 | 6 | 1.004 |
| 5 | 7 | 0.999 |
| 5 | 8 | 0.989 |
| 5 | 9 | 1.012 |
| 5 | 10 | 1.03 |
Calcular a distribuição
Determine a distribuição dos valores medidos. O maior valor medido é 1,03 (grupo de amostra 1, nº de amostra 10). O menor valor medido é 0,9 (grupo de amostra 1, nº de amostra 3).
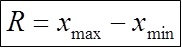
Distribuição = 1,03 - 0,9 = 0,13Calcular a largura da classe:
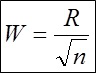
A largura da classe é de 0,13 / √50 = 0,02055480479109446565799280803881. Esse valor é arredondado para 0,02.
Compor as classes
As classes são compostas da seguinte maneira: Tolerância inferior da classe 1 (ou Xmin em caso de Xmin < tolerância inferior) então Classe2 = Classe1 + W e assim por diante. São geradas as seguintes classes:
| Classe 1 | 0,900000 |
| Classe 2 | 0,920000 |
| Classe 3 | 0,940000 |
| Classe 4 | 0,960000 |
| Classe 5 | 0.980000 |
| Classe 6 | 1,000000 |
| Classe 7 | 1,020000 |
Preencher as classes
Os valores das diferentes medidas podem ser agrupados em uma classe se o valor for maior ou igual ao valor de classe e menor do que o valor de classe + a largura da classe. O resultado é:
| Classe | Nº de medições |
| 1 | 1 |
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 12 |
| 6 | 36 |
| 7 | 1 |
Calcular a média
Para cada medição, a diferença em relação à média é calculada e o quadrado das diferenças é somado. Se o primeiro número da amostra tem um valor de medição de 1:
(1 - 0,995850)² = (0,00415)² = 0,0000172225O quadrado das diferenças é calculado e somado para formar uma diferença de quadrados total. No exemplo acima, o total é 1,311734.
Média = desvio padrão - √ 1,311734 /
50 = 0,160000Plotar o gráfico
A figura a seguir exibe o gráfico plotado com os dados acima:
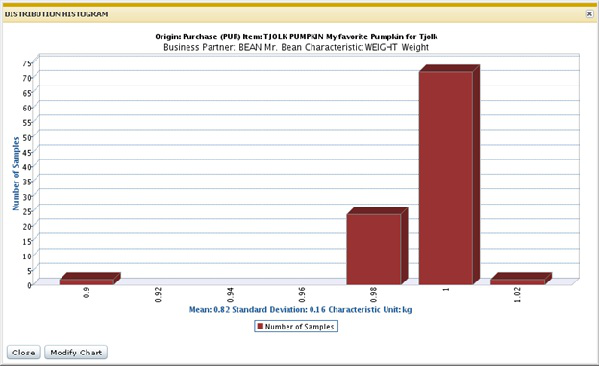
No eixo X é exibida a unidade das características. No entanto, é possível que, para um procedimento de teste padrão específico ou para uma linha de ordem de inspeção, o valor da medição seja expresso em uma unidade diferente que depois é convertida para a unidade de característica.