Méthode de prévision : régression polynomialeInfor LN calcule la prévision de la demande selon la méthode de prévision Régression polynomiale, sur la base d'un polynôme de degré n correspondant aux données d'historique de la demande. Les paramètres relatifs à cette méthode de prévision sont les suivants :
Vous pouvez mettre à jour ces paramètres dans la session Articles plan - Paramètres de prévision (cpdsp1110m000). Le degré du polynôme est indiqué dans le champ Degré de régression polynomiale. Si la case Mise à jour automatique des paramètres de prévision est cochée, Infor LN détermine le degré optimal du polynôme. Demande moyenne corrigée en fonction de la tendance Tout d'abord, les chiffres de demande historique sont ajustés avec la demande moyenne corrigée en fonction de la tendance pour la période concernée. Sans variation saisonnière : DT(t) = DM Avec une variation de tendance linéaire : DT(t) = DC + FT x t Avec une variation de tendance progressive : DT(t) = DB x FT ^ (t-1)DM(t) = DR(t) - TD(t Où :
(*) La demande moyenne est la somme des chiffres d'historique de la demande par période, divisée par le nombre de périodes avec historique de la demande. Coefficients du polynôme Infor LN calcule les coefficients du polynôme avec la méthode de régression polynomiale. Pour plus d'informations sur la régression polynomiale, voir la Rubriques liées. Prévision de la demande Infor LN calcule la demande pour chaque période de prévision en fonction de la demande moyenne (corrigée en fonction de la tendance pour la période en question) augmentée du bruit moyen des périodes passées. Bruit Le bruit est la fluctuation des données de demande par rapport à la tendance qui a été déterminée. Le bruit moyen est calculé pour chaque période de prévision, en fonction des périodes d'historique écoulées depuis un nombre entier de cycles saisonniers. Remarque Si le champ Type de variation saisonnière contient Sans objet, Infor LN suppose l'existence d'un cycle saisonnier fictif avec une longueur de saison pouvant s'étendre jusqu'au quart du nombre de périodes avec demande historique. Exemple La figure 1 montre les données d'historique de la demande pour deux cycles saisonniers comportant 8 périodes de prévision. La période 9 est la période courante. 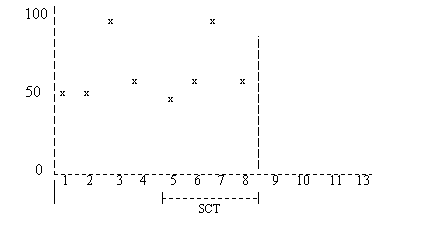 Figure 1
La figure 2 montre le polynôme qui a été déterminé par régression polynomiale : 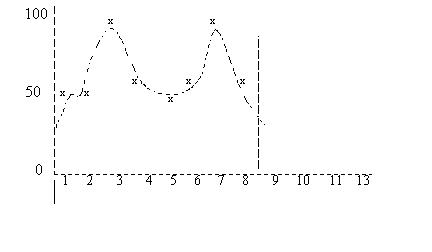 Figure 2 Pour chaque période d'historique, la demande basée sur le polynôme est comparée à la tendance de la demande. Une tendance linéaire est supposée exister ; elle est caractérisée par la formule suivante :
Le bruit moyen issu de ces différence est ajouté à la demande corrigée en fonction de la tendance. Par exemple, le bruit moyen de la période de prévision 9 est la moyenne du bruit des périodes 1 et 5.
Les résultats apparaissent dans la figure 3 : 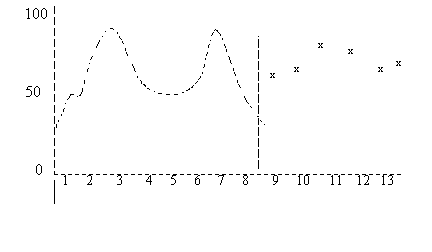 Figure 3
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||