Метод прогнозирования: полиномиальная регрессияСистема LN рассчитывает прогноз спроса в соответствии с методом прогноза Полиномиальная регрессия на основе полинома степени n, соответствующего данным ретроспективы спроса. Соответствующие параметры данного метода прогноза:
Эти параметры можно задать в сеансе Плановые единицы - Параметры прогноза (cpdsp1110m000). Степень полинома указывается в поле Степень полиномиальной регрессии. Если выбран флаг Автообновление параметров прогноза, система LN определяет оптимальную степень полинома. Трендовая корректировка среднего спроса Сначала старые значения спроса корректируются при помощи трендовых корректировок среднего спроса для соответствующего периода. Без сезонного влияния: TD(t) = AV С линейным влиянием тренда: TD(t) = CS + TF * t С прогрессивным влиянием тренда: TD(t) = BS * TF ^ (t-1)DM(t) = AD(t) - TD(t) Где:
(*) Средний спрос - это сумма старых значений спроса по периодам, разделенная на число периодов, в которых имеются данные ретроспективы спроса. Коэффициенты полинома Система LN рассчитывает коэффициенты полинома при помощи метода полиномиальной регрессии. См. Связанные темы в нижней части данного раздела. Прогноз спроса Система LN рассчитывает спрос для каждого периода прогноза на основе трендовой корректировки среднего спроса для рассматриваемого периода, увеличенного на средний шум для значений ретроспективы. Шум Шумом называются флуктуации данных спроса по сравнению с заданным трендом. Средний шум определяется для каждого периода прогноза на основе периодов ретроспективы, отстоящих на целое число сезонных циклов. Примечание Если в поле Тип сезонного влияния указано Не применяется, система LN рассматривает воображаемый сезонный цикл с длиной сезона не более четверти всех периодов с ретроспективой спроса. Пример На рис. 1 показаны данные ретроспективы спроса для двух сезонных циклов, состоящих из 8 периодов прогноза. Период 9 - текущий. 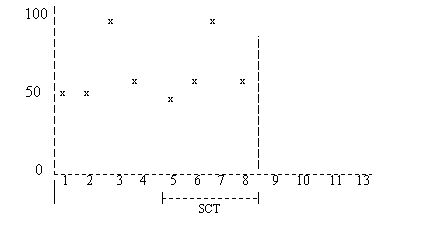 Рис. 1
На рис. 2 показан полином, определенный методом полиномиальной регрессии. 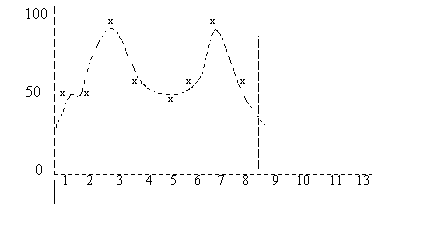 Рис. 2 Для каждого периода ретроспективы основанный на полиноме спрос сравнивается с трендом спроса. Считается, что тренд линейный, описывающийся следующей формулой:
Средний шум, основанный на этих разницах, добавляется к скорректированному по тренду спросу. Например, средний шум для периода прогноза 9 - это средний шум для периодов 1 и 5.
Результат показан на рис. 3. 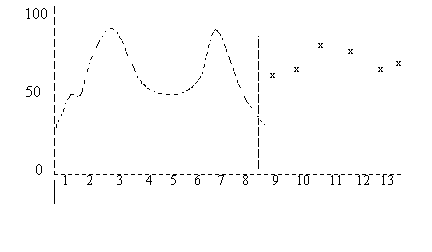 Рис. 3
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||