Forecast method: polynomial regressionLN calculates the demand forecast according to the Polynomial Regression forecast method on the basis of an n'th degree polynom, which matches the historic demand data. The relevant parameters for this forecast method are:
You can maintain these parameters in the Plan Items - Forecast Settings (cpdsp1110m000) session. The polynom's degree is indicated by the Degree for Polynomial Regression field. If the Automatic Update of Forecast Parameters check box is selected, LN determines the polynom's optimum degree. Trend-adjusted average demand First, the historical demand figures are adjusted with the trend-adjusted average demand for the relevant period. Without seasonal influence: TD(t) = AV With a linear trend influence: TD(t) = CS + TF * t With a progressive trend influence: TD(t) = BS * TF ^ (t-1)DM(t) = AD(t) - TD(t) Where:
(*) The average demand is the sum of the historical demand figures by period, divided by the number of periods with demand history. Coefficients of the polynom LN calculates the coefficients of the polynom with the polynomial regression method. See the Related topics for more information about polynomial regression. Demand forecast LN calculates the demand for each forecast period based on the trend-adjusted average demand for the period in question, increased with the average noise in the past. Noise The noise is the fluctuation of the demand data compared to the trend that has been determined. The average noise is determined for each forecast period based on the history periods which are a whole number of seasonal cycles ago. Note If the Type of Seasonal Influence field is Not Applicable, LN assumes a fictitious seasonal cycle with a season length of up to a quarter of the number of periods with historical demand. Example Figure 1 shows the history demand data of two seasonal cycles, which consist of 8 forecast periods. Period 9 is the current period. 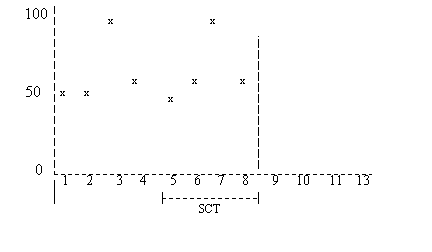 Figure 1
Figure 2 shows the polynom that is determined with polynomial regression. 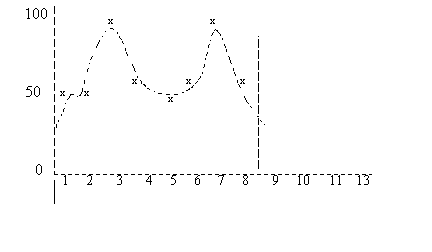 Figure 2 For each history period, the demand based on the polynom is compared to the trend of the demand. A linear trend is assumed to be present, characterized by the following formula:
The average noise based on these differences is added to the trend-adjusted demand. For example, the average noise for forecast period 9 is the average of the noise of periods 1 and 5.
The result is shown in Figure 3. 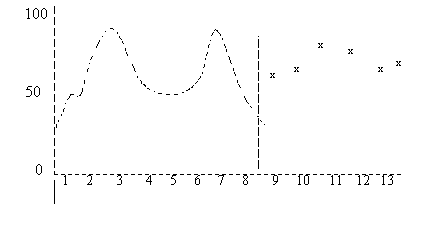 Figure 3
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||