Prognosemethode: polynomische regressieLN berekent de vraagprognose volgens de prognosemethode Polynomische regressie op basis van een n-de-graads polynoom, die overeenkomt met de historische vraaggegevens. De relevante parameters voor deze prognosemethode zijn:
Deze parameters kunt u muteren in de sessie Planartikelen - prognose-instellingen (cpdsp1110m000). De graad van de polynoom wordt aangegeven door het veld Graad polynomische regressie. Als het selectievakje Prognoseparameters automatisch bijwerken is ingeschakeld, bepaalt LN de optimale graad van de polynoom. Voor trend gecorrigeerde gemiddelde vraag Eerst worden de historische vraagcijfers gecorrigeerd met de voor de trend gecorrigeerde gemiddelde vraag van de relevante periode. Zonder seizoensinvloed: TD(t) = AV Met een lineaire trendinvloed: TD(t) = CS + TF * t Met een progressieve trendinvloed: TD(t) = BS * TF ^ (t-1)DM(t) = AD(t) - TD(t) Waarin:
*: De gemiddelde vraag wordt bepaald door de som van de historische vraag per periode te delen door het aantal perioden met vraaghistorie. Coëfficiënten van de polynoom LN berekent de coëfficiënten van de polynoom met de polynomische regressiemethode. Zie Gerelateerde onderwerpen voor meer informatie over polynomische regressie. Vraagprognose LN berekent de vraag van elke prognoseperiode op basis van de voor trends gecorrigeerde gemiddelde vraag van de betreffende periodem, waarbij ook de gemiddelde ruis uit het verleden wordt meegenomen. Ruis Ruis is de schommeling van de vraaggegevens ten opzichte van de vastgestelde trend. De gemiddelde ruis wordt voor elke prognoseperiode bepaald op basis van de historieperioden van een geheel aantal seizoenscycli in het verleden. NB Als het veld Type seizoensinvloed op Niet van toepassing staat, gaat LN uit van een fictieve seizoenscyclus met een seizoenslengte van maximaal een kwart van het aantal perioden met historische vraag. Voorbeeld Figuur 1 toont de historische vraaggegevens van twee seizoenscycli die bestaan uit acht prognoseperioden. Periode 9 is de huidige periode. 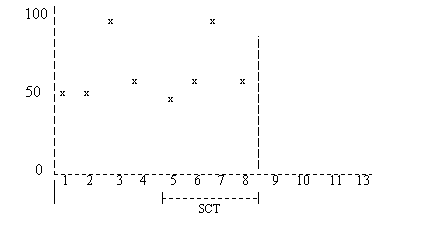 Figuur 1
Figuur 2 toont de polynoom die is bepaald met polynomische regressie. 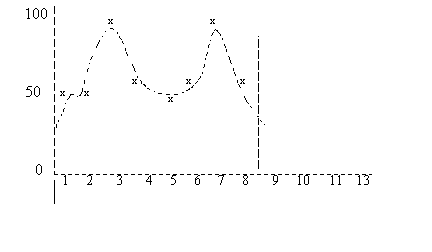 Figuur 2 Voor elke historieperiode wordt de vraag die op de polynoom is gebaseerd, vergeleken met de trend van de vraag. Er wordt vanuit gegaan dat er een lineaire trend is, die wordt gekarakteriseerd met de volgende formule:
De gemiddelde ruis die op deze verschillen is gebaseerd, wordt opgeteld bij de voor trends gecorrigeerde vraag. Zo is bijv. de gemiddelde ruis van prognoseperiode 9 het gemiddelde van de ruis van de perioden 1 en 5.
U ziet het resultaat in figuur 3. 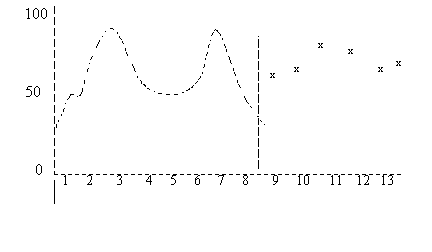 Figuur 3
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||